e constant or Euler's number is a mathematical constant. The e constant is real and irrational number.
e = 2.718281828459...
The e constant is defined as the limit:
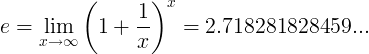
The e constant is defined as the limit:
![]()
The e constant is defined as the infinite series:
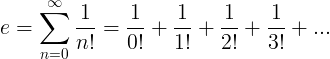
The reciprocal of e is the limit:
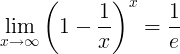
The derivative of the exponential function is the exponential function:
(e x)' = ex
The derivative of the natural logarithm function is the reciprocal function:
(loge x)' = (ln x)' = 1/x
The indefinite integral of the exponential function ex is the exponential function ex.
∫ ex dx = ex+c
The indefinite integral of the natural logarithm function loge x is:
∫ loge x dx = ∫ lnx dx = x ln x - x +c
The definite integral from 1 to e of the reciprocal function 1/x is 1:
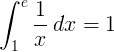
The natural logarithm of a number x is defined as the base e logarithm of x:
ln x = loge x
The exponential function is defined as:
f (x) = exp(x) = ex
The complex number e iθ has the identity:
eiθ = cos(θ) + i sin(θ)
i is the imaginary unit (the square root of -1).
θ is any real number.